A traditional, basic approach in the problems of machine learning is to use a single determined algorithm or model in the implementation of a valid solution. This traditional method is based on creating a pipeline of all the processes that are covered by the development of this algorithm.
This pipeline consists of several phases: ETL processing, data analysis, model implementation and training, results analysis based on determined metrics and other purging mechanisms, and lastly, the launching into production of the model.
Primarily, during the research and implementation phase of the model, one or several determined algorithms are used as a potential solution to the problem given its category. Naturally, regression algorithms will be chosen to predict the outcome of a quantitative variable. In a more elaborate approach, where the number of features is so large that monitored analysis and interpretation of the results takes on a higher degree of complexity, it is possible to split the problem into various phases by using meta algorithms.
In this situation, the cycle of testing, adjusting and error correction is fundamental in the search for the algorithm or model with the correct hyper-parameters.
A parallel solution is the composition of base algorithms and a superior meta algorithm. This set of algorithms forms a stack, where the meta algorithm is the last link in the chain, whereas the base algorithms will be the ones implemented simultaneously to feed their input.
In this architectural approach, base algorithms use different sets of input features; some of them may be shared. In this way, we will have different models for each set of determined features. The way to separate these sets is based on the prior analysis of the data, or failing this, on the intake source .
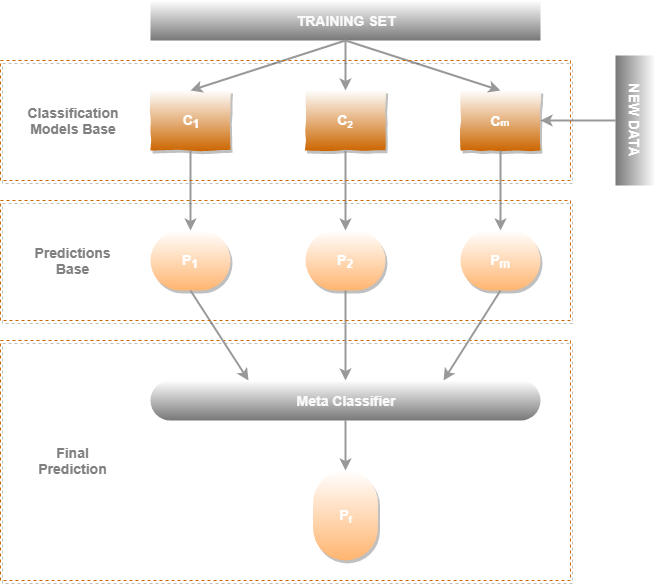
In practice, a non-trivial problem such as the detection of fraudulent transactions or financial fraud, the amount of attributes to be handled can become uncontrollable. Using the meta algorithm structure, a type of algorithm is determined for each data source or set of determined features and to be able to establish which features are essential or can boost the development of the final model.
Moreover, different models can be studied for different sets of attributes and be analysed to improve the correlation between them. This maximises the capacity to select the correct model and set of predominant features in the development of the model.
In this architecture, the meta algorithm uses the percentage of precision or metric associated to each of the base algorithms, using the binary label as a target, in this case, true or false.
In the analysis of meta algorithms it is necessary to use SHAP (SHapely Additive exPlanations) to determine which of the base algorithms is most relevant to produce actual predictions and labels.
SHAP is an approach for explaining the results of the models or algorithms of machine learning. It assimilates game theory with local explanation methods to represent possible expectation-based features. It detects the existing correlation and the value provided by the features in the results of the model.
In the following example, it is possible to observe which attributes contribute best to the learning model.
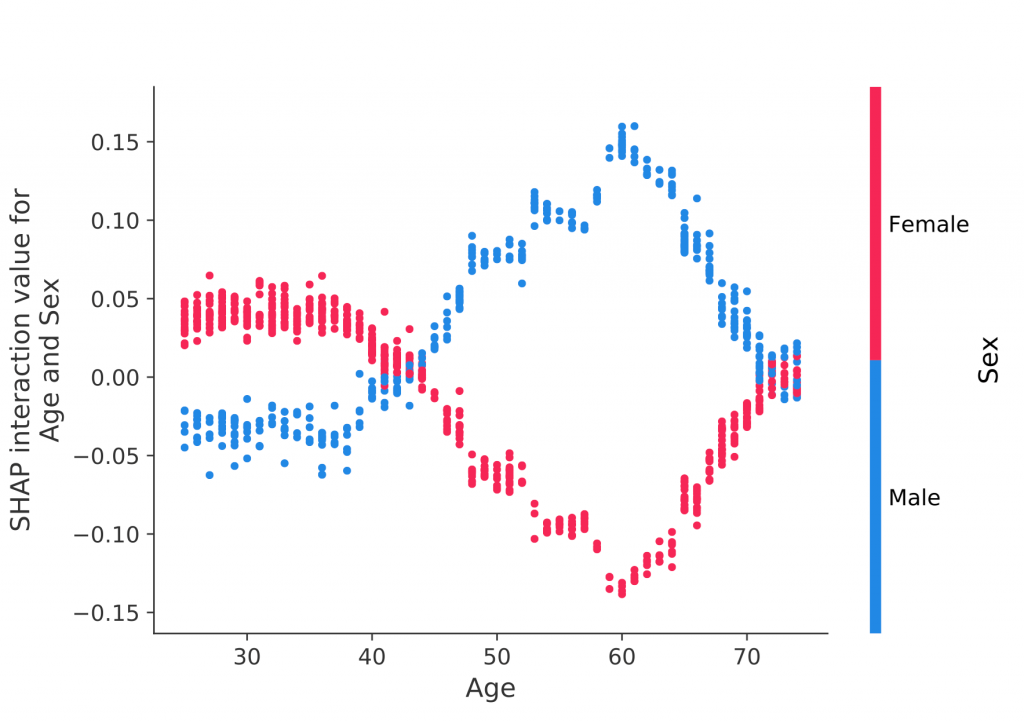
The sex and age features are implicitly correlated in the model’s inference depending on their age range. In this example, a man with an age of approximately 60 will obtain a greater impact on the model’s development. Whereas a female of the same age will not stand out.
Going back to the case of financial fraud detection, this architecture, apart from having the advantages shown, has some disadvantages.
The main disadvantage is presented during the implementation, training and testing phase. This is due to the stack of base algorithms to be implemented and taught. Code development becomes fairly complex, training computationally complicated and we are conditioned by the source and volume of data.
The time necessary for the development of the entire set of algorithms is much longer-lasting than the implementation of traditional measures.
However, as a phase for research, executing batch processes for processing meta algorithms with different configurations of models and duly programmed sets of features, it is possible to achieve solutions to more complex problems.
As assistance for the development of this architecture, Python’s MLxtend library has inherited all the Scikit-Learn algorithms to implement the model stack and feed a principal meta algorithm.
Due to the complexity of this paradigm, it is necessary to start the research phase with simpler solutions. In the principle of parsimony, more well-known as Occam’s razor:
“All things being equal, the simplest solution tends to be the best one.“
This formula applied in the field of statistical and computational learning theory could be expressed as follows:


